Real Estate Research
Featured Study: House Prices Modeling, Prediction and Mapping
The present work investigates spatiotemporal characterization of a residential housing market by means of the house locations in an area of interest and their prices across time. Modeling house prices to build a price index can be a challenge when observed data are not abundant. This composite task is tackled from a geostatistical perspective that enables application of core space-time analysis approaches for the first time in the real estate domain.
In the present analysis, price variability is modeled in the joint space-time continuum rather than purely in space, thus accounting more correctly for the particular characteristics of spatiotemporal geometry in house prices. In addition, the lack of observed data (particularly at the intra-neighborhood level) is mitigated by applying the Bayesian Maximum Entropy (BME) prediction method that enables rigorous integration of informative content from secondary and uncertain soft data sources.
About the Analysis
The study examines residential house prices in Tarrant County, Texas, from January 2009 to December 2012. Observed transaction prices are considered as hard data in the analysis. House sales are general sporadic in both space and time, and often inadequate to provide detail about house prices at the neighborhood level. To this end, the study also employs assessed values from the local property tax office as soft data. The tax-assessed values are released only once a year in the beginning of each year. This is best used as soft information because assessments across properties often exhibit inequity and a lack of uniformity; assessed values often lag transaction prices; and the formal appraisal process is typically not a negotiated arms-length transaction. Soft transaction prices are then derived by regression against the tax values and a series of property characteristics (such as the living area, home age, etc.) that are public information in the Tarrant county assessor’s database.
The study investigates two housing cases using BME that are of high practical interest in real estate research: Case A focuses on a homogeneous subset of sales transactions up to $250K. Market participants (i.e., appraisers, owners, and investors) determine value based on similar comparable properties, therefore Case A examines a practical refinement of the observed data. Case B refers to building a small-scale price index for a neighborhood-sized area.
The following animations depict predicted monthly transaction prices for Case A in a rectangular area of 4700m x 9100m in Tarrant County, and throughout a selected time period that covers the 24 months in 2010-2011. The maps on the left illustrate predicted BME means on a 47x91 grid, and the maps on the right show the corresponding Kriging predictions on the same space-time nodes. The maps are plotted in the same house prices scale that ranges within about $72K - $250K. Unlike Kriging-based results, BME prediction accounts also for the soft information that enables BME to construct a more elaborate profile of house prices behavior in space-time. This is evident in the BME maps that catch spatiotemporal heterogeneities in more detail and clarity than the kriged coarser interpolation among the fewer hard observations.
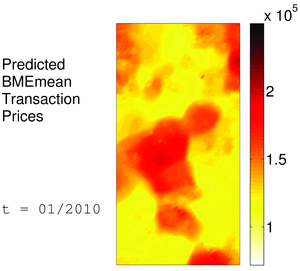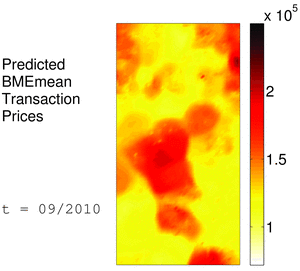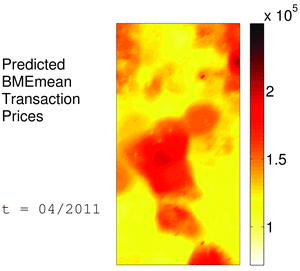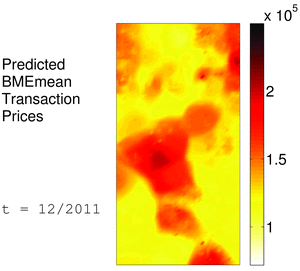

BME performance proves to be valuable in environments with limited observed hard data, where classical geostatistical prediction offers comparatively reduced accuracy. Otherwise, in the presence of abundant observations, classical methodologies were found to offer comparable accuracy at reduced computational burden. Most significantly, the study charts a pathway to gain deeper understanding of market behavior by synthesizing knowledge from multiple sources in a rigorous spatiotemporal geometry context that had previously never been explored in real estate analysis and mapping.
The mapping results demonstrate the local market behavior as it evolves across space and time, and can be valuable tools for assessment, analysis, planning, and management for both real estate researchers and practitioners in housing markets.
Reference
Hayunga D. K., and A. Kolovos. 2016. Geostatistical space–time mapping of house prices using Bayesian maximum entropy. Intl J of Geog Information Science, doi: http://dx.doi.org/10.1080/13658816.2016.1165820.